Strumenti antichi di Proprietà Teorema 
|
SINTESI DI UNA STORIA DEGLI STRUMENTI PER LA MISURA TOPOGRAFICA
Luigi Colombo: Istituto di Topografia, Fotogrammetria
e Geofisica, Politecnico di Milano
Attilio Selvini: Istituto di Geodesia, Topografia e Geofisica
Mineraria, Università di Bologna.
- Premessa
In questa fine del XX secolo che vede la tecnica in genere e le tecnologie
informatiche in particolare fare progressi che nessuno avrebbe potuto
prevedere anche solo un trentennio fa, sembra significativo volgere
uno sguardo al passato per fermare nel tempo immagini e momenti importanti
del percorso strumentale che l'uomo ha ideato e costruito per misurare
l'ambiente che lo circonda. La storia della misura è di per sè
assai affascinante; scrive infatti M. Cunietti sull'operazione di misura:
"... Ma quale elemento della natura ha suggerito all'uomo la
misura? Niente. La misura è tutta quanta opera dell'uomo, non
l'ha rubata a nessuno, non è un'operazione mimetica. Non esiste
una operazione naturale che ci porti ad un numero; il numero è
frutto dell'intervento umano".
E più oltre: "Questo... serve a puntualizzare un elemento
fondamentale della misura: la sua nascita e la sua vita interamante
umane; essa serve all'uomo per trasferire le sue conoscenze scentifiche
nelle sue produzioni tecniche: una volta adempiuto questo compito, i
numeri, quindi le misure, scompaiono, restano solo gli oggetti portatori
dell'impronta dell'uomo".
Fra i mezzi per misurare, certamente un posto di privilegio va riservato
a quelli che hanno permesso all'uomo di ricostruire l'immagine metrica
della Terra: gli strumenti per la geodesia, per la topografia (va ancora
una volta ricordato, che da noi si indica con "Topografia"
- almeno a partire dalla seconda metà del secolo scorso - quella
parte della Geodesia che altri, ad esempio i popoli di lingua tedesca,
chiamano "inferiore". Sebbene la dizione "strumenti geodetici"
possa far pensare a gravimetri o a teodoliti universali, in buona parte
d'Europa tale locuzione ben si adatta a quelli che in Italia sono meglio
conosciuti come strumenti topografici), per l'agrimensura.
Questo articolo vuol essere un sottile filo conduttore che leghi nell'ambito
di due millenni, il pensiero e l'abilità umana, i nomi di inventori
spesso dimenticati o al più citati in modo meccanico senza collocazione
storica, a quegli strumenti che i topografi giornalmente utilizzano
e conservano. Per ragioni espositive, gli strumenti sono stati ripartiti
in tre categorie, anche se certo fra esse vi sono notevoli intersezioni
e correlazioni: la prima riguarda la misura delle direzioni angolari,
la seconda quella delle distanze, la terza infine quella dei dislivelli.
Non saranno dimenticati strumenti accessori e misti, cui si dedicherà
qualche breve nota.
La misura angolare
Probabilmente si deve agli arabi il vocabolo che designa
ancora oggi lo strumento universale per la misura degli angoli. In piena
"età di mezzo" per l'Europa, nelle pianure di Bagdad,
la città delle "Mille e una notte", ai tempi del califfo
Arun er Rascid venne eseguita per la prima volta (dopo l'episodio di
Eratòstene) la misura di un arco meridiano. Non si sa nulla degli
strumenti usati; è però quasi certo che fossero provvisti
di un mezzo collimatore e di un indice ("al idat", in arabo:
qualcuno trascrive "al idadah").
Il termine in arabo passò più tardi in Inghilterra, divenendo
"the alidat". In un teso ivi pubblicato nel 1552, Leonard
Digges parla di "... an instrument called theodolitus";
più tardi il sostantivo diviene "theodolite". Tenendo
conto della pronuncia inglese, effettivamente "the alidat"
e "theodolite" suonano quasi uguali.
Vi è un cenno (ad esempio su "la Filotecnica" vol.
1 anno 1, 1931, in una notarella di D. Argentieri) su altra possibile
etimologia del termine teodolite. Questa si farebbe discendere dalle
altre tre parole greche:
"thea-hodos-lithos", cioè "vedere-via-pietra";
L'Argentieri dà poco credito a tale etimo, anche se pare che
gli antenati del teodolite avessero basamento di pietra (?). Non è
possibile invece pensare ad un accenno alla "pietra" da cui
proviene il vetro delle ottiche di collimazione, perchè i primi
teodoliti avevano solo delle diottre, essendo precedenti all'invenzione
del cannocchiale.
Qualche dato ora sulla evoluzione storica del teodolite.
Le prime misure angolari indirette nell'antichità, sono fatte
attraverso l'ombra dello "gnomone" o con metodi similari:
si pensi alla nota misura di Erastòtene, prima accennata. La
determinazione della direzione - quindi misura angolare - per
fissare il cardine ("cardo"), veniva fatta in età romana
con gnomone e cerchio tracciato sul terreno circostante. Dall'asta semplice,
detta anche "asta d'ombra", si passò in seguito al
"regolo di mira" che era costituito da un'asta inclinata per
traguardare la sommità di un oggetto, e fornita alle due estremità
di fili a piombo. Il passo successivo fu un regolo costituito da due
aste collegate fra loro ad angolo retto (fig. 1) che probabilmente originò
il "baculo" (fig. 2).

Figura 1 - Misura con la squadra
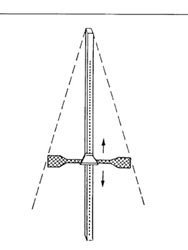
Figura 2 - Sistema del "bastone di Giacobbe"
Dice Cosimo Bartoli nell'opera citata in bibliografia:
"Per fare il baculo, apparecchisi un regolo quadro per tutti
versi di legno durissimo e atto a non torcere, o pigliasi di ottone
lungo quanto ci piace;... dividasi poi detto regolo in alcune parti
uguali fra loro dieci otto sei... e si chiami questo regolo AB.
Facciasi di poi un altro regolo simile: ma lungo solamente quanto una
delle parti: in le quali dividesti il primo regolo AB.....e chiamasi
questo regolo minore CD come si può vedere nel disegno..."
(fig. 3)

Figura 3 - Il "baculo" o "giacobea"
Il baculo veniva impiegato per misurare la distanza fra
punti inaccessibili, non direttamente angoli: ma è chiaro che
la misura era basata su un angolo parallattico, variabile in funzione
della distanza.
Vere misure angolari sono invece eseguite con il "quadrato geometrico",
di cui molti trattatisti medievali parlano sotto i nomi di "quadratum
mediclinorum", "instrumentum gnomonicum", eccettera.
Sembra che il "quadrato" compaia addirittura verso l'anno
100 a.C.: era costituito da quattro aste a telaio o da una tavoletta
quadrata (fig. 4)
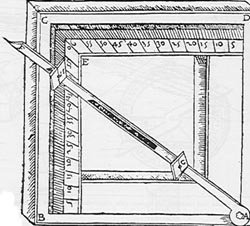
Figura 4 - Il quadrato geometrico in una delle forme
diffuse nel 1500
Ua riga (dioptra, alidada - termine arabo, come s'è
visto - regula, mediclinium) disposta secondo una diagonale e girevole
su di un vertice del quadrato, permetteva le collimazioni (fig. 5).
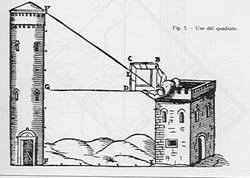
Figura 5 - Uso del quadrato
Notizie particolareggiate sull'uso del quadrato geometrico
vengono date da S. Belli, in "Libro da misurar con la vista",
Venezia, 1569. Al Belli viene ascritta l'antenata della "Tavoletta
pretoriana" (v. par. 5) che l'autore avrebbe mutuata appunto da
un quadrato geometrico; nell'opera del Belli vi è infatti la
"misura col tamburo" (fig. 6) e certamente tale arnese militare
è già qui "in nuce" un fondamento di tavoletta.

Figura 6 - La misura "col tamburo", antesignano
della "tavoletta".
E' il classico problema dell'intersezione in avanti.
Altro tipo di "quadrato" viene descritto da
Cosimo Bartoli, in "Del modo di misurare le distanze, ecc.",
Venezia 1589. Questo è sicuramente un goniometro (fig. 7) capace
tra l'altro di misurare angoli di altezza; a lui fa seguito altro predecessore
del teodolite in grado di esser disposto su un supporto piano e provvisto
di bussola (fig. 8). Non è però storicamente il primo
goniometro completo.
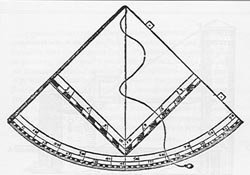
Figura 7 - Il "quadrante geometrico" o "quadrato",
descritto dal Bartoli
Figura 8 - Strumento topografico descritto dal Bartoli
nel 1589, usato per rilevamenti di grandi estensioni di terreno.
Il primo strumento capace di misurare angoli orizzontali
e verticali è infatti il "Polimetrum" (fig. 9) costruito
nel 1512 da Martin Waldssemüller, topografo e cartografo renano.
Lo strumento era anche provvisto di bussola e il suo costruttore rilevò
con esso la carta della Renania Superiore (1513, Strassburg)
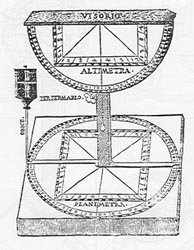
Figura 9 - Il Polimetrum, strumento del secolo XVI
da un'incisione in legno del 1512
Waldseemüller descrive lo strumento in appendice
alla "Margarita Philosophica" di Gregor Reisch. Questo goniometro
venne subito utilizzato da altri topografi, ad esempio da Walter Lud
e da Martin Ringmann, per il rilevamento della carta della Lorena.
Come collimatore il "Polimetrum" aveva un lungo tubo con due
fessure alle estremità, che poteva essere disposto anche in posizione
orizzontale e ivi fissato tramite apposita vite.
Come detto all'inizio, è Leonard Digges ad usare per la prima
volta nella storia il nome "theodolitus"; egli ed il fratello
Thomas erano matematici e costruttori di strumenti, ed insegnavano "Pantometria"
(Topografia) a Londra. Forse lo strumento che più assomigli ad
un vero teodolite è però quello costruito da Joshua Habermel
in Germania nel 1576, completo di bussola e treppiede.
Legati allo sviluppo del teodolite sono due importanti elementi costitutivi,
se pur non indispensabili come organi fondamentali: il cannocchiale
(da sostituire alla semplice diottra) e il mezzo per frazionare i piccoli
intervalli della graduazione dei cerchi.
Del 1542 è il dispositivo del portoghese Pedro Nunez (1492-1577);
si trattava di 46 cerchi concentrici, ognuno dei quali suddiviso in
(n - 1) intervalli rispetto al precedente. Dal nome dell'inventore è
derivato il noto termine "nonio" che ha dominato la scena
dei frazionatori di intervallo fino ai giorni nostri, del tutto erroneamente.
Solo i francesi hanno sempre usato il termine corretto: verniero.
E' infatti Pierre Vernier (meglio, Peter Werner olandese, 1580-1637)
a costruire nel 1631 e diffondere poi l'uso del dispositivo nella forma
conosciuta (una scala divisa in n parti, affacciata su intervalli di
graduazione di n - 1 elementi). Ma l'invenzione è di parecchio
anteriore, dovendosi ascrivere al matematico Clavius (1593), che ne
fece uso per il tracciamento (non per la misura) di angoli sulla
carta.
Circa l'invenzione del cannocchiale per usi astronomici, le cose sono
note. Il primo strumento è certamente quello del fiammingo Hans
Lipperhey (1560-1619), vetraio ed ottico, che compare nei Paesi Bassi
nel 1608. Il nostro Galileo ne ha notizia e nel 1609 realizza la nota
versione, usabile praticamente, che inizia la storia delle osservazioni
celesti. Di Johannes Kepler (1571-1630) è l'altra versione detta
appunto "astronomica", costruita dal gesuita Christoph Scheiner
nel 1611, seguita nello stesso anno dalla versione "terrestre"
a immagine diritta , sempre di Kepler.
Ma è l'italiano Generini a usare la prima volta, nel 1630, il
cannocchiale kepleriano per "collimare", cioè con oculare
a reticolo.
L'inglese William Gascoigne nel 1640 usa il cannocchiale collimatore
per il suo "quadrante". Sarà seguito nel 1670 dal francese
Picard (1620-1682) e da qui l'uso si diffonde anche nel settore della
topografia.
Gascoigne va menzionato anche per un terzo organo accessorio: è
infatti lui l'inventore della vite micrometrica. Per tutto il
XVII secolo l'ingrandimento del cannocchiale è assai modesto
(9 ÷ 20 x) e le immagini sono affette da aberrazioni assai vistose.
Tutto cambia nel "secolo dei lumi"; infatti l'inglese Moore
Hall (1704-1771) inventa nel 1729 l'obbiettivo acromatico, costruito
più tardi nel 1785 da John Dollond. Non sarà male a questo
punto ricordare che per oltre un secolo, con il conforto del parere
di Newton corredato da una dimostrazione del tutto errata del grande
scienziato, nessun costruttore aveva nemmeno tentato di fabbricare obbiettivi
di questo tipo perchè la correzione dell'aberrazione di cromatismo
era stata dichiarata impossibile. In verità Dollond era stato
preceduto almeno nella confutazione matematica dell'errore newtoniano
da Eulero, che scriveva nel 1769, riferendosi però a circa quindici
anni prima: "Quod ergo incommodum a diversa radiorum natura
oriundum adeo grave vel summo Neutono est visum, instrumenta dioptrica
nullo modo ab hanc causam non opus sit ad telescopica Catoptrica confugere.
(Quell'inconveniente dovuto alla diversa natura dei raggi che anche
al sommo Newton sembrò così grave da giudicare impossibile
il liberarne gli strumenti diottrici, ormai è certo che si può
facilmente eliminare, almeno per quanto riguarda il margine iridato,
a cui specialmente Newton si riferiva; cosicchè almeno per questa
causa non vi è più ragione di ricorrere a telescopi catadiottrici.
E Dolland, dodici anni prima di questa nota su "Dioptricae"
aveva infatti realizzato i suoi obbiettivi privi dell'aberrazione di
cromatismo.
Gli studi sulla tecnica produttiva del vetro ottico, dovuti a Josef
Fraunhofer (1787-1826) conducono alla disponibilità di vetri
per lenti che permettono un vero progresso nella costruzione di cannocchiali
collimatori per strumenti topografici: questi si diffondono così
nelle forme sostanzialmente ancora oggi adottate.
John Sisson, inglese, realizza nel 1730 uno dei primi teodoliti "moderni";
i tempi sono maturi e il progresso si fa avanti veloce.
Nel 1783 Jesse Ramsden (1735-1800) inventa l'oculare dallo stesso nome
e un anno più tardi il microscopio a vite nicrometrica; vent'anni
prima (1763) egli aveva già prodotto la "macchina a dividere".
Di qualche anno precedente è quella di Hidley costruita a New
York. Il metodo meccanico di divisione dei cerchi è però
ancora precedente, ascrivendosi al noto fisico Hooke nel 1684.
Circa gli oculari, prima di Ramsden va menzionato quello dell'olandese
Christian Huygens (1629-1695) nel 1684, cioè nello stesso anno
in cui Hooke insegna a dividere correttamente le scale.
Nel 1803, Georg Von Reichenbach (1771-1826) costruisce la macchina a
dividere con copia da un cerchio fondamentale, che ispirerà i
lavori successivi del nostro Ignazio Porro.
Il francese J.C. Borda, ben noto astronomo (1733-1799) studia il cerchio
"ripetitore" con i relaviti assi: tale cerchio verrà
poi messo a punto da altro noto meccanico francese, Etienne Lenoir (1744-1832),
di cui si parlerà ancora a proposito dei livelli.
Il cerchio avrà un diametro di 33 cm; altro cerchio sarà
costruito nel 1804 da Reichenbach (fig.10) e poi altro ancora da Repsold
di Amburgo (ma sarà già il 1830)
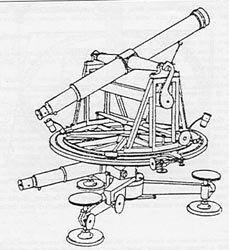
Figura 10 - L'universale di Reichenbach (1804)
Nel 1784 Ramsden prepara un teodolite con il cerchio di
ben 1 jarda di diametro (fig. 11), con precisione di 1" su osservazioni
a punti distanti almeno 10 miglia e tre microscopi di lettura.
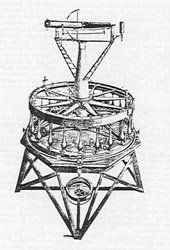
Figura 11 - il grande Teodolite di Ramsden costruito
nel 1784
Siamo ormai alla produzione rigorosamente scentifica dei
teodoliti. Il "centramento forzato" è del tedesco Breithaupt
(1840); ma questo sistema diverrà d'uso pratico solo ottant'anni
più tardi coi lavori di H. Wild presso la Carl Zeiss di Jena.
Si arriva così al nostro Ignazio Porro (1801-1875), cui si devono
non poche e sostanziali novità.
Il teodolite diventa per sua opera "tacheometro" anzi "cleps":
si passa dai grossi cerchi in metallo, con graduazione su bordo d'argento,
a cerchi di piccolo diametro in vetro ottico "racchiusi" in
scatole metalliche, sì da essere al riparo da ingiurie meccaniche
ed atmosferiche. Nasce il microscopio a stima, il cannocchiale di forte
ingrandimento e soprattuto "centralmente anallattico". Lo
strumento è ora adatto non solo all'astronomo o al geodeta ma
anche al comune topografo, che potrà abbandonare il triplometro
e tavoletta (fig. 12). E' una prima, vera rivoluzione: la seconda scatterà
dopo quasi un secolo, per opera di Heinrich Wild (1877 - 1951) con la
media per via ottica delle letture a lembi opposti al cerchio e il cannocchiale
di lunghezza costante. Il secondo dopoguerra porterà solo progressi
minori, a parte le nuove ottiche trattate secondo il processo di Smakula
e già usate nel 1937/38: saranno le letture "semidigitali"
dei cerchi, i compensatori per le letture zenitali, i cerchi a doppia
graduazione. Tutto sommato poca cosa a fronte della terza, forse definitiva,
rivoluzione incombente già alla fine degli anni Sessanta: la
misura elettronica delle direzioni. Ma questa non è più
storia, bensì cronaca.

Figura 12 - Disegno originale di uno dei "Cleps"
di Porro (1860)
3. La misura delle distanze
La misura diretta delle grandezze afferenti alla
classe delle lunghezze è stata certamente la prima nella storia
dell'uomo. I vari "campioni" di lunghezza furono dapprima
elementi o porzioni di arti di colui che misurava: braccio (cubitus
per i romani), dito, palmo, spanna, piede. E poi vennero unità
maggiori, come il passo (semplice o doppio), la tesa (distanza
fra le punte del dito medio a braccia spalancate); ad esse si affiancano
misure d'altro genere, come il versus (lunghezza del solco che
un bue fa in un solo tratto, pari per i romani a 120 e per i greci a
100 piedi), e il famoso stadion che tanto fece discutere a proposito
della misura di Erathostenes Pentathlos. Pare si riferisse al tratto
di distanza che un uomo robusto poteva fare di corsa, ritenuto di 1000
piedi (circa 300 m).
Da queste unità di misura naturali, certamente non precise
per via delle differenze fra persona e persona, sorsero con il divenire
dei tempi altre unità convenzionali, costituite da regoli
di legno o metallo. Queste si stabilizzarono con gli anni, e Vitruvio
ne parla nel libroIII del suo "De Architectura". I nuovi campioni
erano rigidi, come aste o canne, o flessibili e pieghevoli come catene,
nastri, funi.
Funi per misura vennero usate dai Babilonesi, Egizi, Ebrei, Greci, Romani,
Arabi. Erone indica quale sia l'uso corretto delle funi; egli afferma
che per evitare le variazioni di lunghezza è opportuno tendere
ripetutamente le funi fra due pali, lasciandole in tensione e strofinandole
con cera e resina.
La catena venne impiegata da Ebrei, Greci, Arabi, Cinesi.
Il suo uso fu però sporadico; il materiale era generalmente ferro.
I nastri vennero assai più tardi, allorchè si pensò
di avvolgere le funi sui rulli. Tipica è la "cassetta metallica"
di Joseph Furtenbach (1644), antisegnana delle odierne rotelle metriche.
La necessità di impiegare elementi autoregistratori fu sentita
sicuramente al tempo di Roma; Erone e Vitruvio parlano di ciò
nei loro scritti. Dice il primo nel suo "Della Diottra": "...
I nostri predecessori discussero su alcuni metodi, secondo i quali è
possibile sostituire la cattiva e lenta misura della distanza per mezzo
di funi e catene col far girare una ruota ...".
Non si sa bene quando e da chi furono costruiti i primi odometri:
le più antiche descrizioni conosciute sono dei due autori sopra
citati.
L'odometro di Erone (fig. 13) differisce da quello di Vitruvio (fig.
14) per forma, non per sostanza. Giulio Capitolino, nell'inventario
dei beni dell'imperatore romano Marco Aurelio Commodo (192 d.C.) cita
"carri per misurare percorsi".

Figura
13 - Odometro di Erone

Figura 14 - Odometro di Vitruvio
Solo però con Leonardo Da Vinci (1452-1529) ricompaiono
gli odometri e i contapassi per uomo e cavallo. Dal VXI secolo in poi,
apparecchi autoregistratori si diffondo soprattutto in Europa Centrale,
a scopo cartografico. I primi rilevamenti infatti furono eseguiti misurando
le distanze con gli odometri, le direzioni con la bussola. Rodolfo II
concede nel 1583 un privilegio di dieci anni a Christopher Schissler
per il rilevamento e la cartografia dell'intero paese; così viene
fatto anche il rilievo della Sassonia (1712-1731).
La misura diretta è lunga, costosa, richiede si percorra
con un campione il tratto da misurare; la misura indiretta è
più complessa, almeno concettualmente: sconosciuta nell'antichità
classica, appare come primo barlume negli scritti del monaco Gerberto
di Aurillac (circa 930-1003), poi Papa Silvestro II. Nella sua geometria
tratta fra l'altro del modo di misurare le altezze, le lunghezze,
le larghezze e le profondità usando l'astrolabio, lo specchio,
l'asta pitagorica.
In verità, metodi che si possono ritenere indiretti erano stati
applicati anche nell'età classica, con la cosiddetta asta
di mira e con l'asta d'ombra.
Con riferimento alle figg. 15, 16, 17 si può vedere come
queste fossero regoli di legno e le misure basate sulla similitudine
di triangoli

Figura
15 - Asta di misura

Figura 16 - Asta d'ombra
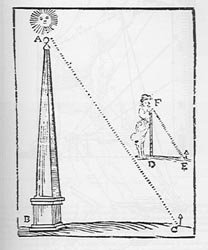
Figura
17 - Misure con l'asta d'ombra
L'asta d'ombra non è altro che il già citato
gnomone.
Dalle aste semplici si passò all'insieme di due aste collegate
ad angolo retto; fra queste va citato, come distanziometro indiretto
il baculo o giacobea o bastone di Giacobbe (fig.
2).
Ne parla il Bartoli ("Del modo di misurare le distanze: le superfici,
i corpi, le piante, le province, le prospettive e tutte le altre cose
terrene", Venezia 1564), già citato in precedenza.
L'uso del baculo è illustrato in centinaia di figure su trattati
italiani e stranieri dei secoli XVI e XVII (figg. 18 e 19).

Figura 18 - Misura di distanze col bastone di Giacobbe
o baculo

Figura 19 - Misura di altezza col baculo
E dopo questo venne la misura ottica, allorchè
furono disponibili i cannocchiali. E' infatti solo dopo la comparsa
del cannocchiale kepleriano che si incominciano a precisare i metodi
che poi, variamente realizzati ed interpretati, si dilateranno fino
ad oggi metodi basati sulla formazione di un angolo parallatico (costante
o variabile, ma più spesso del primo tipo, per la semplicità
dei calcoli connessi), di un angolo cioè che fosse capace di
legare insieme distanza incognita e campione noto di lunghezza. Il primo
a costruire, nella seconda metà del '600, un dispositivo di tal
genere è Geminiano Montanari (Astronomo della Repubblica Veneta,
che nel 1674 descrisse la sua "livella diottrica", dotata
di cannocchiale con oculare positivo e di molte coppie di fili distanziometrici
da usare con stadia verticale a scopi), ma la realizzazione pratica
che storicamente è accertato sia stata usata per prima e largamente
applicata al rilevamento di terreni anche accidentali, è quella
dell'inglese William Green. Costui costruì e brevettò
un secolo dopo quello del Montanari, nel 1778, un cannocchiale distanziometrico
munito di reticolo a due tratti, incisi su lastrine di vetro rettificabili.
Con esso si doveva usare una stadia a scopi mobili, tenuta normale alla
visuale.
All'incirca di uguale data sono gli esperimenti di M. De La Hire, francese
(1774) e del tedesco A. Brander (1764), cui si aggiunge nel 1774 l'inglese
J. Watt.
Ma è solo con la costruzione del cannocchiale distanziometrico
del bavarese Georg Von Reichenbach (1771-1827) che il metodo, seppure
fra incertezze, ostilità, grandi speranze, entusiasmi peraltro
non giustificati dai modesti risultati ottenuti con le prime esperienze,
entrerà nella pratica del topografo.
Von Reichenbac costruì nel 1810, valendosi tra l'altro della
cooperazione di J. Von Fraunhofer (1787-1827), un cannocchiale con reticolo
a due punte rettificabili, a grande angolo parallattico, da usarsi con
stadia graduata e senza scopi: questa fu una grande innovazione pratica,
seguita dall'introduzione (non giustificata teoricamente dal R.) della
costante additiva. Il genio e la lunga esperienza di Ignazio Porro consentiranno
pochi decenni più avanti non solo la giustificazione teorica
della "formula" di Reichenbach, ma anche la costruzione, da
parte dello stesso Porro, dapprima del cannocchiale da lui detto stereogonico,
in cui il vertice dell'angolo parallatico coincide con il punto
nodale esterno dell'obbiettivo del cannocchiale, e subito dopo del cannocchiale
centralmente anallattico, in cui tale vertice coincide rigorosamente
con il centro del cannocchiale, eliminando così la costante additiva
e rendendo monomiale la formula della distanza desunta indirettamente.
Dovrà passare ancora quasi un secolo prima che H. Wild costruisca
il cannocchiale di lungezza costante praticamente anallattico, nel quale
cioè il vertice dell'angolo parallattico oscilla di pochi millimetri
intorno al centro dello strumento, per cui la costante additiva è
nulla solo per una data distanza, mentre è praticametne nulla
per tutte le altre al di là delle distanze di alcuni metri,
che è inutile misurare indirettamente.
Nell'intervallo di quasi un secolo fra i lavori del Porro e quelli di
Wild s'era manifestata la necessità, grazie anche allo sviluppo
enorme assunto dalla topografia celerimetrica, cioè numerica,
rispetto ai vecchi metodi di rilevamento diretto del terreno, di disporre
di formule semplicemente moltiplicative e prive di funzioni trigonometriche
anche quando la visuale del cannocchiale distanziometrico fosse inclinata.
Il primo a pensare a questo e a realizzare uno strumento "autoriduttore",
capace cioè in ogni caso di fornire il valore della distanza
orizzontale senza eseguire prodotti trigonometrici e soprattutto senza
misurare angoli verticali, fu ancora il Porro.
Egli costruì allo scopo il cannocchiale stenallattico, in
cui la focale variava con l'inclinazione dell'asse di collimazione sì
da far rimanere indipendente dall'angolo di altezza la costante distanziometrica.
Lo strumento del Porro non ebbe fortuna; tutta la seconda metà
del XIX secolo fu un fiorire di invenzioni e proposte per la costruzione
di autoriduttori fondati su due metodi distinti: le scale tangenziali
ed i reticoli a diagrammi. In verità, un antesignano dei "riduttori"
venne ideato già nella seconda metà del XVIII secolo da
Lodovico Perini (fig. 20). Lo strumento, di legno o metallo era strutturato
come il "diagramma di Orlandi" di un secolo e mezzo dopo;
aveva serie di semicerchi concentrici (di diametro corrispondente a
varie distanze) ed un'asta collimatrice (di inclinazione variabile).

Figura
20 - L'autoriduttore di Perini
L'uso è intuitivo,dato che l'intersezione fra un
semicerchio e la riga obliqua permette di leggere sulla proiezione a
tal punto, nella parte dei diametri comuni, la distanza ridotta. Capostipite
dei moderni distanziometri riduttori (non totalmente autoriduttori,
richiedenti cioè alcune operazioni manuali) è lo strumento
proposto nel 1866 dal francese E. Sanguet. Si tratta in realtà
di un clisimetro con scala tangenziale verticale: fatte due letture
alla stadia con due diverse inclinazioni del cannocchiale, sì
che per esempio la differenza delle pendenze sia di 1/100, la distanza
viene data dal prodotto dell'intervallo di stadia per l'inverso di tale
differenza, cioè nel caso esemplificato per 100.
Segue nell'anno successivo lo strumento di Wagner, costruito dalla casa
tedesca Fennel; nel 1889 il riduttore di Charnot con scala orizzontale;
nel 1898 quello di Vogler, costruito da Hildebrandt a Freiberg; nel
1900 altro strumento di Doergens, poi infine nel 1912 quello del francese
Balu, prodotto dalla Kern di Aarau.
Solo in Sanguet ha successo, soprattutto nel paese d'origine, e viene
prodotto in migliaia di esemplari: esso ispirerà ancora nel secondo
dopoguerra, il TARI della Salmoiraghi, anche se qui la scala tangengiale
è disposta sul cerchio verticale.
I riduttori e gli autoriduttori con reticolo di varia foggia, per fare
in modo che il prodotto della costante strumentale K per cos2
alfa possa rimanere costante con l'elevazione
del cannocchiale (K = f/r: o varia f, come nello strumento
del Porro, o varia r, distanza fra i tratti del reticolo) nascono
un pò più tardi di quelli a scala tangenziale.
La prima proposta è degli italiani Roncagli e Urbani (1890) a
fili mobili (soluzione che verrà adottata molto più tardi
da Kern). Su questo, R. Von Hammer (1858-1925) - professore a Stoccarda
- progetta il primo vero autoriduttore di questa classe che avrà
gran successo; sarà costruito da Fennel nel 1900 e gli verrà
applicato il cannocchiale centralmente anallattico del Porro.
Nel 1919 il norvegese Dahl ne studia e propone un miglioramento; per
oscuri motivi però solo nel 1932 viene costruito un prototipo
e la serie, essa pure di successo e dotata del nuovo cannocchiale a
lunghezza costante progettato da H. Wild per Zeiss, vede la luce con
gran ritardo nel 1942. Il Dahlta (Dahl Tachymeter) non avrà
tuttavia forte diffusione, per via dello stato di guerra in atto.
Il geometra svizzero Leemann nel 1930 brevetta una variante dell'autoriduttore
a fili, su cui Kern costruirà nel 1929 il DKR e nel 1946 il DKRM.
Su tale brevetto, con varianti modeste, è fondato anche il Wild
RDS nel 1951, il TA-D1 della ungherese MOM (1959), il russo TA-2 (1959)
ed infine l'RTa4 Zeiss di Oberkopchen del 1967.
La misura ottica delle distanze è possibile anche usando stadia
orizzontale e cannocchiale con reticolo a tratti distanziometrici verticali;
una variante che prescinde dal reticolo a tratti, è quella con
cuneo prismatico. L'idea della "doppia immagine" dovuta al
cuneo, risale allo statunitense Richards, nel 1894, rimasta però
senza applicazione pratica. L'idea era stata già in precedenza
applicata a un telemetro, in altra versione, dagli inglesi A. Barr e
W. Stroud, precisamente nel 1888.
Nel 1922, il topografo svizzero R. Bosshardt (1884-1967) ottiene il
brevetto per un dispositivo capace di autoridurre le distanze inclinate,
mediante letture su stadia orizzontale. E' del 1924 il prototipo Redta
(Reduktions Tachymeter) Bosshardt-Zeiss. Per diffondere anche presso
i vari organismi pubblici del centro-Europa la propria invenzione, Bosshardt
pubblica nel 1930 un volumetto e addirittura Otto Von Gruber ne fa oggetto
di minuziose ricerche. La precisione del nuovo autoriduttore a diasporametro
è stupefacente per i tempi. Nasceranno poi, sull'onda del successo
del Redta Zeiss e con le solite varianti il DK-RT Kern (1947) e l'RDH
Wild (1950).
Poche parole sui telemetri. E' Brander, nel 1781, a proporre un telemetro
a specchi, seguito nel 1790 da Ramsden con telemetro a prismi e semimmagini.
Solo nel 1888 i già citati Barr e Stroud realizzano uno strumento
adatto all'uso topografico; ma è Carl Pulfrich, il padre dello
stereoscopio (1858-1927), a produrre nel 1900 alla Carl Zeiss di Jena
il primo telemetro steroscopico che tanta diffusione avrà per
scopi militari, mentre saranno modeste le sue applicazioni in campo
topografico.Va ricordato che Pulfrich lavorò su un brevetto del
francese Grousillier del 1893.
La misura delle basi geodetiche, introdotta da W. Snell, Snellius (1591-1926)
richiedeva l'uso di longimetri diretti di precisione ben superiore alle
catene, ai nastri, alle ruote dentate. Snellius usò a Leiden
nel 1615 delle pertiche di legno appoggiate al suolo; altrettanto fecero
Norwood nel 1633 per la misura della base fra Londra e York e poi Pichard
nel 1669. Era allora ignorata l'influenza della temperatura e dell'umidità
e i risultati furono modesti.
Solo all'inizio del XVIII secolo Cassini usò aste metalliche,
misurando la temperatura e quindi tenendo conto delle variazioni di
lunghezza: gli errori furono però ancora rilevanti per il consueto
appoggio sul terreno delle aste, dato che i supporti erano allora ignorati.
Questi furono introdotti da R.G. Boskovic (1711-1787) e dal suo confratello
G.B. Beccaria: il primo per la misura della base dell'Appia, il secondo
per quella di Rivoli. Le pertiche sono di legno, disposte su cavalletti
e rese orizzontali con cunei di legno, nonchè allineate con teodolite.
La misura delle basi diventa "scientifica" persò solo
con Reggio, Oriani e De Cesaris, i tre astronomi di Brera che nel 1788
usarono pertiche di ferro a T su travi di legno per la misura della
base di Somma lungo il corso del Ticino; tutti gli accorgimenti noti
sono qui utilizzati ed infatti le successive misure della base, l'ultima
nel 1878 per opera dell'IGMI, ne confermano la bontà originaria.
Sarà F.W. Bessel (1784-1846) ad usare le aste bimetalliche, ideate
peraltro da Borda, impiegando cunei di vetro e sfruttando così
le diverse dilatazioni di ferro e zinco come termometro interno.
Le aste a tratti, proposte dal Porro con i suoi telescopi panfocali
sono usate dall'americano Hassler; è infine il proferssore svedese
M. Eduard Jäderin dell'Università di Stoccolma a proporre
come basimetri, nel 1878, fili o nastri di acciaio in tensione, con
piastrine terminali e indici su treppiede.
L'apparato verrà perfezionato quando, nel 1900, Benoit e Guillaume
introdurranno la lega di ferro e nichelio detta invar, con coefficiente
di dilatazione lineare pari a circa 1/10 di quello dell'acciaio.
Passerà ancora mezzo secolo e si giungerà finalmente alla
misura elettronica delle distanze, sia lunghe che corte, sia di precisione
tecnica che geodetica.
Certo la possibilità di misurare le distanze con la luce fu per
diversi secoli il sogno degli studiosi. Il primo a tentare conteporaneamente
la misura della velocità della luce, e nota questa, la misura
per via ottica della distanza, fu Galileo nel 1648. Egli dispose due
lampade a 6 e a 3 miglia di distanza, tentando una modulazione della
luce con il rapido passaggio delle mani (dei suoi collaboratori) davanti
alle sorgenti; ma il tentantivo cadde perchè allora si ignorava
che, a quelle distanze, il tempo necessario per passare le mani e così
ottenere la successione buio-luce, era enormemente grande rispetto a
quello che in realtà sarebbe stato necessario. Infatti, mentre
il suono viaggia nell'aria a crica 350 m/s ed a 3 e 6 miglia
di distanza una variazione di emissione di suoni sarebbe facilmente
avvertibile, la luce (ma Galileo, appunto, non lo sapeva) corre circa
900.000 volte più in fretta! Se ne rese conto però, trent'anni
più tardi, Roemer, che nel 1676 misurò con metedo astronomico
tale velocità utilizzando i satelliti di Giove, sia pure con
un errore del 25%.
Bradley ne ottenne all'incirca il corretto valore nel 1725, finchè
si giunse alla nota esperienza di Fizeau, che nel 1849, con un modulatore
a ruota dentata (e cioè stavolta con metodo terrestre) trovò
un valore scostantesi di circa il 5‰ da quello che noi oggi conosciamo.
Il metodo di Fizeau può a ragione ritenersi come il primo sistema
adatto alla misura della distanza con luce modulata. Fra gli esperimenti
per misurare la velocità della luce si ricordano ancora quello
di Foucault (1862) e, sessant'anni più tardi, quello di Michelson
in California: Foucault usò uno specchio ruotante, Michelson
una prisma. Ad ogni modo, il primo distanziometro elettro-ottico del
mondo fu costruito sperimentalmente in Unione Sovietica da Lebedev,
Balakoff e Wafiadi, però su brevetto (datato 1933) di un altro
studioso russo, Trofimuk.
Altri brevetti ottennero il francese Toulon nel 1937 e lo statunitense
Wolff nel 1939.
Gustav Förstner e Karl Cantz, sperimentarono un distanziometro
a impulsi poco prima della seconda guerra mondiale; nel 1938 misurarono
la distanza fra terra e un aereo, a circa 100 km, con incertezza di
1 km, ridotta dopo altre esperienze a 50 metri. La Lutwaffe (l'arma
aerea del Reich) impedì ulteriori sviluppi civili dello strumento,
ritenendo sufficiente a scopi bellici la precisione raggiunta.
Sempre Förstner, con Walther Brucklacher, costruisce il FuG 103,
capace di misurare elettronicamente dislivelli con precisione di 2 m.
Occorre però arrivare fino al secondo dopoguerra perchè,
su lavori pubblicati nel 1940 negli "Annali della Fisica"
a Berlino, lo svedese Erik Bergstrand possa costruire il primo distanziometro
elettronico utilizzabile commercialmente chiamato Geodimeter, contrazione
della frase Geodetic Distance Meter.
Il prototipo del geodimetro, non ancora industrializzato, misurò
nel 1950 sino a 30 km (di notte, con lampade a vapori di mercurio).
Nel 1953, il primo strumento commerciale, pesante 110 kg e atto a fornire
la misura in 40 minuti, venne acquistato dal Dipartimento della Difesa
degli USA. Il più grosso difetto era costituito allora dal sistema
riflettore, uno specchio piano. Per caso, un impiegato della casa produttrice,
la AGA di Lidingö, ricordò che pochi anni prima la marina
svedese aveva usato come riflettori dei prismi di Porro modificati,
in grado di riflettere il raggio ottico parallelamente alla direzione
di incidenza entro un range di circa 20°. Ne nacque così
il "Corner Cube", oggi ben conosciuto.
Nel 1955 appare il geodimetro modello 2° e l'anno seguente il 3°.
Il geodimetro 4° del 1958, pesa "solo" 34 kg, misura in
dieci minuti, ha una portata di 1 km alla luce solare; portata che quattro
anni più tardi diventa di ben 20 km. Ormai il progresso dell'elettronica
incalza; nel 1965 la versione 6 è transistorizzata e nel 1967
il mod. 8 ha portante laser e distanze utili di 130 km.
Al geodimetro degli anni '50 segue nel 1959, uno strumento a microonde,
capace quindi di attraversare con la portante foschie, piogge, ostacoli
leggeri (come fogliame), ma con lo svantaggio di richiedere all'altro
estremo della distanza una ricetrasmittente anzichè un semplice
riflettore passivo, come nel caso dello struemento ad onde portanti
luminose. L'apparato, del sudafricano Wadley, prese il nome di Tellurometer.
Si noti che sia il nome dello strumento di Bergstand che quello
di Wadley contengano la radice della parola terra: il primo con
derivazione dal greco (ge), il secondo dal latino (tellus).
I primi strumenti dei due tipi erano dunque ingombranti e pesanti, richiedendo
inoltre una notevole alimentazione per il loro funzionamento. Le operazioni
di misura avvenivano in modo semimanuale, con conteggi finali semplici
ma fastidiosi, sulla scorta di formulari completati nel corso delle
misure stesse.
In pratica tali strumenti erano utilizzabili solo dalle organizzazioni
statali o regionali addette al rilevamento delle grandi reti di appoggio.
Ma il rapido progresso fa sì che già nel 1960 i geodimetri
risultino semplificati ed in grado di rendere servigi anche al topografo
oltre che al geodeta. Infine nel 1968 compare sul mercato, costruito
in tandem da Wild e dalla francese Sércel (per la parte elettronica),
il primo pratico e leggero Distomat DI 10, accoppiabile al teodolite
e con portata massima di 1 km, adatto al rilevamento delle poligonali
e a quello di dettaglio. La sua costruzione verrà resa possibile
dalla scoperta del diodo all'arseniuro di Gallio (1967), che apre le
porte alla strumentazione attuale.
4. La misura dei dislivelli
La storia del livello è legata indissolubilmente
a quella dell'adduzione di acqua per irrigazione e per uso potabile.
Si ricordano ad esempio l'acquedotto sotterraneo di Siloè a
Gerusalemme, costruito nel 700 a.C., lungo circa 510 m, con dislivello
di 10 m e pianta a S; il tunnel di Samo 525 c.C. ed infine gli innumerevoli
acquedotti romani sparsi per tutto l'impero, dall'Africa, all'Asia,
alla Britannia. Tutte queste opere presupponevano la misura di dislivelli
con buona precisione.
Vitruvio, nel suo "Dell'architettura", capo VI, libro VIII,
dice (nella traduzione del cardinale D. Barbaro, Venezia 1567): "...il
livello... (intendendo qui la livellazione, n.d.A.) si suol
fare con tali strumenti, con il traguardo, con il livello ad acqua
e con quello strumento che si chiamava corobate, e con questo più
diligentemente e sicuramente si livella, perchè il traguardo
e il livello ad acqua fallano. Il corobate è una asta lunga
piedi 20, la quale ha le braccia piegate...".
Il chorobates era quindi un'asta di legno di circa 6 m
di lunghezza (fig. 21) con una faccia piana nella quale si realizzava
un incavo a canaletto, che andava riempito d'acqua. Agli estremi dell'asta,
due bracci ortogonali configurano nell'insieme una specie di panca,
alla quale erano sospesi due fili a piombo per parte, come traguardi.
Questi servivano a rendere verticali i fianchi dell'asta e quindi
orizzontale la canaletta per l'acqua (ammesso che i due bracci fossero
sufficientemente ortogonali all'asta).

Figura 21 - Il "Chorobates"
Il corobate è quindi il livello preferito dai
romani, che però usavano anche il livello ad acqua (non si
sa in quale forma, ma comunque questo doveva prevedere i due classici
bicchieri all'estremità di un tubo di collegamento) ed il "traguardo",
detto anche "Lychnia" o "Lampada", probabilmente
per la forma (fig. 22).
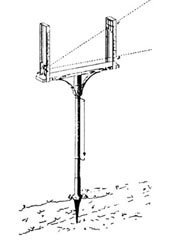
Figura
22 - Una ricostruzione della "Lychnia"
Il corobate era però il livello più sensibile
e più preciso; la cosa più interessante (e poco conosciuta)
è che Vitruvio, parlandone, dice quanto segue: "...Ma
chi leggerà i libri di Archimede forse dirà che non
si può direttamente livellare con l'acqua, perciocchè
a lui piace che l'acqua non sia piana, ma di figura sferica; e ivi
avrà il centro suo, dove il mondo ha il suo, ma questo è
vero sia l'acqua piana o sferica...". E' sorprendente non
tanto che Archimede abbia pensato e scritto della terra sferica e
dell'acqua (in quiete) disposta secondo quella che oggi chiamiamo
superficie equipotenziale, bensì che, oltre duecento anni dopo
la sua morte cruenta, Vitruvio si rammentasse e ne parlasse a sua
volta. Ciò significa che il dibattito scientifico era rimasto
vivo nei due secoli trascorsi e che i Romani non erano quella gente
pratica che la tradizione ci ha rimandato, ma un popolo capace anche
di riflessioni e di osservazioni non solo empiriche.
Riflessioni che però scompariranno, almeno nel settore della
scienza, per oltre un millennio: quello dei "secoli bui".
Si tramanda solo il ricordo e giusto l'uso del livello ad acqua, del
quale nel 1660 il Padre Riccioli fa un'attenta descrizione fornendo
anche le precisioni raggiungibili nelle livellazioni sino a circa
10 km: nemmeno trascurabile, essendo indicata in 10 cm.
Nel 1629 , G. Branca aveva inventato il livello idrostatico, usato
ancora oggi dai "solini" per la posa dei pavimenti.
Ed ecco nascere, in concomitanza con i grandi lavori geodetici, nuovi
livelli che si possono definire automatici, dato che sono asserviti
ad una massa pesante. Sono tali quelli di J. Picard (1620-1682), Huyghens,
De La Hire (figg. 23-24).
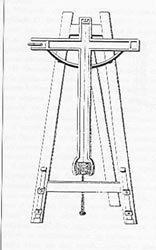
Figura
23 - Livello di Picard
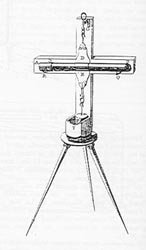
Figura 24 - Livello di Huygens
Come si vede, sono sostanzialmente aste con peso all'estremità,
collegate con una diottra a traguardi. Il "pendolo" di Picard
in particolare è lungo circa 1.3 m (anticipa così la
pari lunghezza, anche se "virtuale", dei moderni compensatori
meccanici, ad esempio del livello Zeiss Ni 1).
E' per primo Alain Malesson Mallet (1630-1706) ad unire un cannocchiale
collimatore (nel 1702) ad un livello a bolla. A questo proposito,
benchè la cosa non sia certa, la livella a bolla entro fiala
torica si ascrive nel 1662 al meccanico parigino J. Thévenot
che forse è anche il primo costruttore del livello detto appunto
"a bolla". Thévenot scrive infatti nel 1666 sul "Journal
des savants", di una "... machine nouvelle pour conduite
des eaux, pour les batiments, pour la navigation et pour la plupart
des autres arts".
La livella a bolla sferica è del meccanico Johann Mayer
di Gottinga (1770). La livella torica descritta e costruita da Thèvenot,
per decenni di incerta fattura e di grosse dimensioni, acquista forma
accettbile solo alla fine del '700, allorchè viene costruito
il primo livello a bolla definibile "moderno". Esso è
opera di Antoine Chézy (1718-1798) ed è del 1770 circa
(fig. 25).

Figura 25 - Il livello di Chézy
Ma solo qualche decennio più tardi, all'inizio
dell'Ottocento, Pierre Marie Thomas Egault, ingegnere capo della napoleonica
scuola di "ponts et Chaussées", lavorando sulla scia
delle indicazioni di Chézy e Borda, costruisce il vero livello
a cannocchiale a livella (fissa alla traversa) che durerà sino
alla fine della seconda guerra mondiale, cioè per un secolo
e mezzo. Lo strumento è descritto puntualmente dall'inventore
in una memoria del 1806, che si riferisce alla nuova rete di distribuzione
idrica per la città di Parigi, dal titolo: "Description
et usage d'un niveau à lunette et a bulle d'air qui donne toujours
l'horizon".
L'ultima costruzione di successo nel settore dei livelli, è
quella di Etienne Lenoir (1744-1832); di questo "livello a cerchio"
(fig. 26) fa uso intenso il servizio di "Ponti e massicciate",
cui si deve anche l'introduzione nelle livellazioni delle stadie "parlanti"
- cioè graduate - al posto delle mire a scopo.
Porro, col suo genio, costruisce un livello di scarsa fortuna, anche
se del tutto nuovo rispetto a Egault e Chézy.
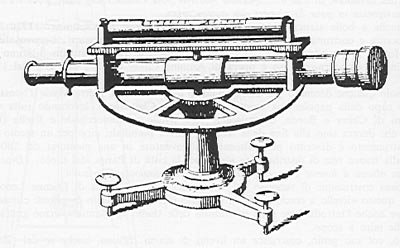
Figura 26 - Il livello di Lenoir
Occorrerà però attendere i lavori di Wild
presso la Car Zeiss, per vedere novità nel settore dei livelli:
lo strumento a livella fissa al cannocchiale(che è di lunghezza
costante) e che durerà sino ai giorni nostri, per essere soppiantato
(a partire dal 1950) dai livelli a orizzontamento automatico, fra
i cui precursori possono essere citati quelli di Picard e di Huyghens
e, in epoca più vicina , quello di Goulier a pendolo.
Poche cose aggiuntive,: la livella a bolla reversibile è di
Amsler (1857), la vite di elevazione è di Sickler, meccanico
di Karlsruhe (fine settecento).
Di modesta importanza i molti livelli realizzati fra la fine del XIX
e l'inizio del XX secolo: livelli a doppia curvatura, a bolla reversibile,
a visuale reciproca; tentativi più che altro per ottenere risultati
più rapidi e precisi, magari a prezzo di modalità operative
anche complesse. Ma le differenze di quota si possono determinare
anche con il teodolite: l'idea di utilizzare distanze zenitali a questo
fine risale a Picard, che l'applicò nel corso di lavori di
livellazione sulla Senna. Egli eseguì una "livellazione
trigonometrica" a visuali reciproche fra la torre Sud di Notre-Dame
ed il chiostro dei cappuccini di Sévres.
E' invece J. Cassini a fare osservazioni di pressione e temperatura
per stabilire le quote dei monti della Linguadoca, dei Pirenei, dell'Auvergne,
introducendo così la "livellazione barometrica".
5. Gli strumenti minori
Queste poche righe illustrative sono nulla, in confronto
alle congerie di strumenti, dispositivi, acessori che il topografo
ha - specie nell'ultimo secolo - utilizzato per la misura e il rilevamento.
Si ricorderanno qui solo i principali.
Dello squadro si potrebbe scrivere a lungo, partendo dalla groma
romana con tutte le sue trasformazioni , sino a quei "bussoli"
o "bossoli" che tanta importanza assunsero nel Setto-Ottocento
(figg. 27-28) e che proprio in questi secoli cominciarono a trovare
concorrenti ottici.

Figura
27 - Squadri del XVI secolo
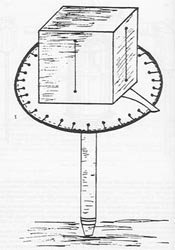
Figura 28 - Squadro "a cubo" con cerchio
graduato
E' per primo il meccanico londinese John Adams (1720-1773) a costruire
lo squadro a specchi che ne porta il nome: la doppia riflessione ne
è il principio informatore. Il fisico inglese H. Wollastone
(1766-1828) preferisce agli specchi il prisma ; nel 1812 costruisce
lo squadro omonimo ben noto, che ancora oggi viene prodotto ed impiegato.
E poi verranno i prismi di Porro, di Bauerfeind (1851) a Monaco di
Baviera, quello pentagonale di Prandtl del 1890, le croci di prismi,
il prisma "universale" del nostro Jadanza.
Il "quadrato geometrico", già citato nel paragrafo
sui teodoliti, fa pensare che il Belli, che lo descrive nel "Libro
del misurare colla vista" (Venezia, 1569) sia forse l'inventore
della "tavoletta", così come già si disse
al punto 2.
In realtà, il goniografo così celebre, che ancora oggi
qualche azienda produce, viene descritto per la prima volta da Gemma
Frisius (1508-1555) nelle sue lezioni all'università di Lovanio
nel 1553. Sicuramente l'astronomo olandese ne avrà costruito
un esemplare; del resto anche Abel Foullon aveva usato nel 1551 il
suo "holométre" (fig. 29) come elemento per il rilievo
in campagna.